Fungsi

Fungsi yang dimaksudkan dalam materi matematika ini berbeda dengan definisi fungsi dalam artian secara umum. Fungsi dalam matematika adalah suatu relasi yang menghubungkan setiap anggota x dalam suatu himpunan yang disebut daerah asal (Domain) dengan suatu nilai tunggal f(x) dari suatu himpunan kedua yang disebut daerah kawan (Kodomain). Himpunan nilai yang diperoleh dari relasi tersebut disebut daerah hasil ( Range).
Pada fungsi, terdapat beberapa istilah penting, di antaranya:
- Domain yaitu daerah asal fungsi f dilambangkan dengan Df.
- Kodomain yaitu daerah kawan fungsi f dilambangkan dengan Kf.
- Range yaitu daerah hasil yang merupakan himpunan bagian dari kodomain. Range fungsi fdilambangkan dengan Rf.
Sifat-sifat fungsi matematika antara lain :
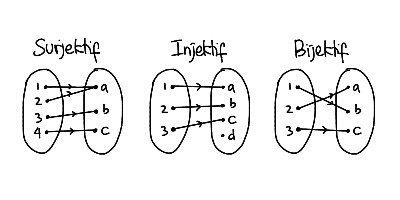
- Fungsi Injektif
Sifat fungsi yang pertama adalah injektif atau juga disebut fungsi satu-satu. Pemetaan (fungsi) f : A → B dikatakan satu-satu atau injektif, jika untuk setiap unsur x1 dan x2 di yang dipetakan sama oleh f, yaitu f(x1) = f(x2) berlaku x1 = x2. - Fungsi Surjektif
Sifat fungsi matematika selanjutnya adalah surjektif.
Fungsi f: A → B disebut fungsi kepada atau fungsi surjektif jika dan hanya jika untuk sembarang b dalam kodomain B terdapat paling tidak satu a dalam domain A sehingga berlaku f(a) = b. Dengan kata lain, suatu kodomain fungsi surjektif sama dengan kisarannya (range). - Fungsi Bijektif
Sifat fungsi matematika yang terakhir ada;ah bijektif. Suatu pemetaan f: A→B sedemikian rupa sehingga f merupakan fungsi yang injektif dan surjektif sekaligus, maka dikatakan “f adalah fungsi yang bijektif” atau “ A dan B berada dalam korespondensi satu-satu.
Jenis-jenis Fungsi dalam Matematika
- Fungsi Linear
Jenis pertama adalah fugsi linear. Fungsi pada bilangan real yang didefinisikan : f(x) = ax + b, a dan b konstan dengan a ≠ 0 disebut fungsi linear - Fungsi Konstan
Untuk lebih memudahkan anda untuk memahami jenis fungsi yang kedua ini, kami berikan contoh. Misal f:A→B adalah fungsi di dalam A maka fungsi f disebut fugsi konstan jika dan hanya jika jangkauan dari f hanya terdiri dari satu anggota. - Fungsi Identitas
Jenis fungsi berikutnya adalah fungsi identitas. Contoh: f:A→B adalah fungsi dari A ke B maka f disebut fungsi identitas jika dan hanya jika range f = kodomain atau f(A)=B. - Fungsi Kuadrat
Jenis fungsi matematika yang terakhir adalah fungsi kuadrat. Fungsi f: R→R yang ditentukan oleh rumus f(x) = ax2 + bx + c dengan a,b,c ∈ R dan a ≠ 0 disebut fungsi kuadrat.

No comments:
Post a Comment